Problem Set 03

Problem Set 03

1. The Subtractor Function

We've already shown the successor function f(n) = n + 1 Turing Machine computable in class. Now consider the following function:

f(n) = n - 1, for all natural numbers n > 1.

Show that f is Turing Machine Computable by constructing a Turing Machine that computes it--i.e., give a flow graph of the instruction set to solve the function for any such n. (10)

2. The Easy Doubler

Show that the following function is Turing Machine Computable by constructing a Turing Machine that computes it--i.e., give a flow graph of the instruction set to solve the function for non-zero natural numbers n, m, and p such that (n + m) > p. (20)

f(n) = n + n

[Hint: Recall the flow graph we gave to show binary addition--f(n,m) = n + m, n,m > 0--in class Turing Machine computable.]

3. The Ugly Doubler

Turing's Theorem--that there exists a Turing Machine that can compute any function computable by any Turing Machine--demonstrates that for any given Turing Machine computable function there are at least two Turing Machine's that compute it. Indeed, we can prove that there are countably infinitely many Turing Machines that compute any Turing Machine computable function.

Of any two Turing Machines TM-1 and TM-2 that compute the same function, let us say that TM-1 is more elegant than TM-2 iff TM-1 requires fewer states in its flow-graph than TM-2. We might add that TM-2 is uglier than TM-1 if it requires more states to do the same thing.

The Ugly Doubler (pdf) is ugly indeed. It requires a total of 17 states to compute the function f(n)=2n, x>0. Write the flow graph of a less ugly Turing Machine that computes the same function. Note that some of the states are obviously eliminable, while more dramatic cuts might be made by reconsidering the basic strategy. The most elegant solution (a mere 6 states!) of the problem I've yet seen is the Ariel McCree Solution:

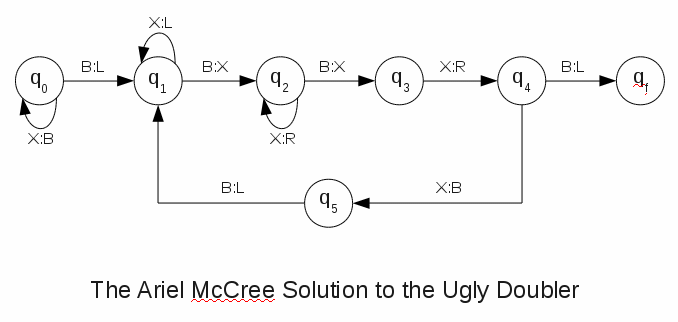
The Ariel McCree Solution to the Ugly Doubler

Whatever your solution, be sure to run your Turing Machine on limiting input (n=1) as well as other test cases (n=3, say) to check whether it works in general! (20)