The Divided Line

Introduction

Two crucial points of the Platonic Dialogues--alluded to but not made explicit in the Symposium--are the Doctrine of the Forms and the Divided Line. These are not essential to understanding the achievement in intellectual history the Symposium represents, exactly, but they are helpful to fully grasp Socrates' speech and several of Diotima's most important points about love.

Background

One of the deeper puzzles with which the Greeks and everyone since has wrestled is the problem of change. How, that is, is change possible? An animal, for instance, is born, thereby coming into existence, grows, thereby changing, and dies, thereby going out of existence. Even things we consider permanent, like mountains and rivers, are apparently constantly changing. There are several alternative solutions to the puzzle, for either

1) Any changes we perceive are an illusion; the world as it is in itself is permanent and unchanging.

• The presocratic philosopher Parmenides argued that all is one. The universe must be one and unchanging. All 'changes' are really illusions.
• Parmenides' student Xeno used his justly famous "Xeno's Paradoxes" like Achilles and the Tortoise to argue that change is impossible.

Or

2) Any permanence we perceive is an illusion; the world as it is in itself is constantly changing.

• The presocratic philosopher Heraclitus famously assserted that "one can never step in the same river twice" and proposed the Doctrine of the Flux as an account of the fundamental nature of reality.

Or

3) Any permanence or change we perceive are illusions; the world as it is in itself makes up the world as we perceive it but with different objects (particles or substances) obeying different rules (laws).

• The presocratics known as the Atomists--including Leucippus and Democritus and later culminating in the Roman Leucretius famous six-book Latin hexameter poem De Rerum Natura or On the Nature of Things--explored this alternative.
• This is arguably a crude expression of a basic tenet of contemporary particle physics and Quantum Mechanics.

In various dialogues, including especially the Phaedo and the Republic, Plato constructs a somewhat complicated but extraordinarily intellectually beautiful variation on the first option.

The Doctrine of the Forms

Consider two red balls. We say that the two red balls objectively resemble one another because there is some thing they have in common. What is that thing? More generally, in virtue of what do particular objects resemble one another? This is the Problem of Universals: Two particulars presumably resemble each other because they are instances of a universal. Yet what is this universal?

Plato proposes that the universal of which the red balls partake or to which they resemble--and in virtue of which they resemble one another--is itself an object, a form. Forms are

• Unchanging,
• Eternal,
• Abstract, in the sense of being intelligible but not perceptible,
• Divine,
• Fundamental, in the sense that everything we perceive is caused by the forms, and,
• Perfect, in the sense that they are without qualification what their instances are only with qualification.

Indeed, any property one can imagine is in reality a form. So, for example,

• All dogs are dogs because they share the property of being dogs, but they share the property of being dogs because they partake to lesser or greater degree in the form of dogness;
• All chairs are chairs because they share the property of being chairs, but they share the property of being chairs because they more or less partake in the form of chairness;
• All persons are persons because they share the property of personhood, which is just to say that particular persons are such insofar as they partake in the form of personhood.

Thus the world as it is in itself is essentially parmenidean: The real world consists of the eternal, unchanging, and perfect forms. The world as we perceive it is heraclitean: A world of constant change or flux according to approximate or qualified resemblance to the forms.

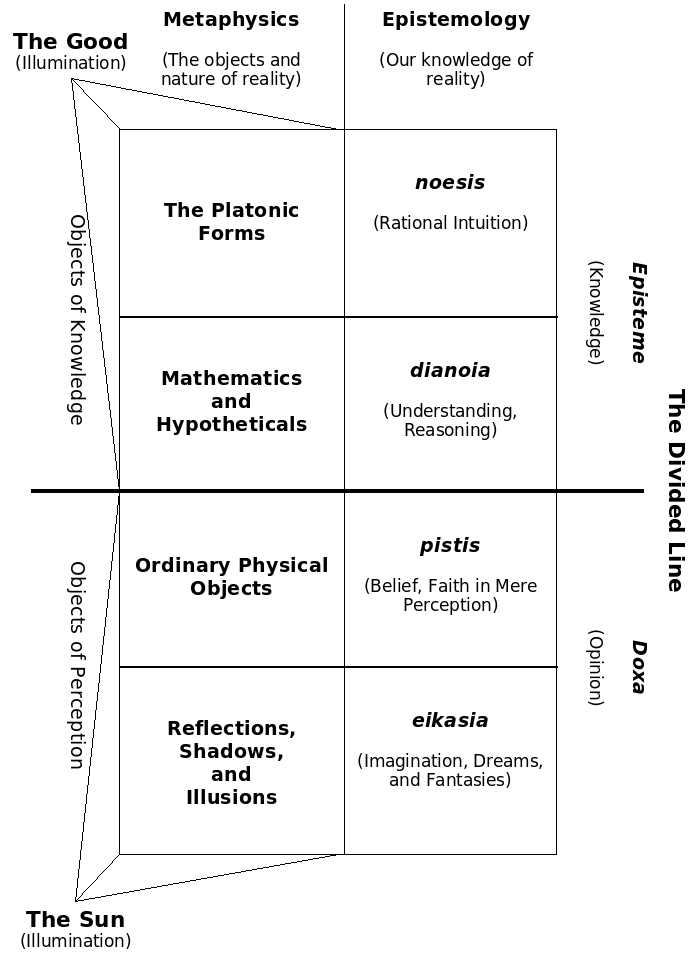
To be sure, the Doctrine of the Forms raises as many questions as it answers. The most pressing problem is how we go about apprehending these forms. Plato offers the Divided Line (Republic 490d) as a way of grasping his solution.

The Divided Line

I represent the Divided Line in a graphic below, but first here are the relevant passages from the Republic, Book VI, 509d and following.

“Conceive then,” said I, “as we were saying, that there are these two entities, and that one of them is sovereign over the intelligible order and region and the other over the world of the eye-ball, not to say the sky-ball, but let that pass. You surely apprehend the two types, the visible and the intelligible.”

“I do.”

“Represent them then, as it were, by a line divided into two unequal sections and cut each section again in the same ratio (the section, that is, of the visible and that of the intelligible order), and then as an expression of the ratio of their comparative clearness and obscurity you will have, as one of the sections of the visible world, images. By images I mean, first, shadows, and then reflections in water and on surfaces of dense, smooth and bright texture, and everything of that kind, if you apprehend.”

“I do.”

“As the second section assume that of which this is a likeness or an image, that is, the animals about us and all plants and the whole class of objects made by man.”

“I so assume it,” he said.

“Would you be willing to say,” said I, “that the division in respect of reality and truth or the opposite is expressed by the proportion:1 as is the opinable to the knowable so is the likeness to that 510b of which it is a likeness?”

“I certainly would.”

“Consider then again the way in which we are to make the division of the intelligible section.”

“In what way?”

“By the distinction that there is one section of it which the soul is compelled to investigate by treating as images the things imitated in the former division, and by means of assumptions from which it proceeds not up to a first principle but down to a conclusion, while there is another section in which it advances from its assumption to a beginning or principle that transcends assumption, and in which it makes no use of the images employed by the other section, relying on ideas3 only and progressing systematically through ideas.”

“I don't fully understand4 what you mean by this,” he said.

“Well, I will try again,” said I,” for you will better understand after this preamble. For I think you are aware that students of geometry and reckoning and such subjects first postulate the odd and the even and the various figures and three kinds of angles and other things akin to these in each branch of science, regard them as known, and, treating them as absolute assumptions, do not deign to render any further account of them5 to themselves or others, taking it for granted that they are obvious to everybody. They take their start from these, and pursuing the inquiry from this point on consistently, conclude with that for the investigation of which they set out.”

“Certainly,” he said, “I know that.”

“And do you not also know that they further make use of the visible forms and talk about them, though they are not thinking of them but of those things of which they are a likeness, pursuing their inquiry for the sake of the square as such and the diagonal as such, and not for the sake of the image of it which they draw? And so in all cases. The very things which they mould and draw, which have shadows and images of themselves in water, these things they treat in their turn7 as only images, but what they really seek is to get sight of those realities which can be seen only by the mind.”

“True,” he said.

“This then is the class that I described as intelligible, it is true, but with the reservation first that the soul is compelled to employ assumptions in the investigation of it, not proceeding to a first principle because of its inability to extricate itself from and rise above its assumptions, and second, that it uses as images or likenesses the very objects that are themselves copied and adumbrated by the class below them, and that in comparison with these latter3 are esteemed as clear and held in honor.”

“I understand,” said he, “that you are speaking of what falls under geometry and the kindred arts.”

“Understand then,” said I, “that by the other section of the intelligible I mean that which the reason itself lays hold of by the power of dialectics,6 treating its assumptions not as absolute beginnings but literally as hypotheses, underpinnings, footings, and springboards so to speak, to enable it to rise to that which requires no assumption and is the starting-point of all, and after attaining to that again taking hold of the first dependencies from it, so to proceed downward to the conclusion, making no use whatever of any object of sense but only of pure ideas moving on through ideas to ideas and ending with ideas.”

“I understand,” he said; “not fully, for it is no slight task that you appear to have in mind, but I do understand that you mean to distinguish the aspect of reality and the intelligible, which is contemplated by the power of dialectic, as something truer and more exact than the object of the so-called arts and sciences whose assumptions are arbitrary starting-points. And though it is true that those who contemplate them are compelled to use their understanding and not their senses, yet because they do not go back to the beginning in the study of them but start from assumptions you do not think they possess true intelligence about them although the things themselves are intelligibles when apprehended in conjunction with a first principle. And I think you call the mental habit of geometers and their like mind or understanding and not reason because you regard understanding as something intermediate between opinion and reason.”

“Your interpretation is quite sufficient,” I said; “and now, answering to these four sections, assume these four affections occurring in the soul: intellection or reason for the highest, understanding for the second; assign belief to the third, and to the last picture-thinking or conjecture, and arrange them in a proportion, considering that they participate in clearness and precision in the same degree as their objects partake of truth and reality.”

“I understand,” he said; “I concur and arrange them as you bid.”

We can represent all this in a fairly condensed graphic as follows: